Das Newtonverfahren zur Lösung nichtlinearer Gleichungen

In den letzten Wochen habe ich mich mit einem mathematischen Verfahren zu Lösung von nichtlinearen Gleichungen und Gleichungssystemen befasst. In diesem Beitrag möchte ich meine Erkenntnisse dokumentieren. Ich verwende die Werkzeuge “Microsoft Excel” und “gnuplot” (siehe Präsentation am Ende des Beitrags). Gnuplot ist ein kostenloses und vielseitiges Programm zur Darstellung von Funktionsgraphen und Messdaten (Plotting):

http://www.gnuplot.info/

Für welche Arten von Gleichungen ist das Newtonverfahren geeignet?

Ich betrachte Gleichungen, die sich in die allgemeine Form einer Polynomgleichung überführen lassen:

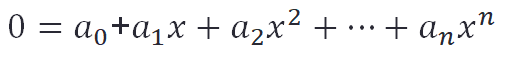
Polynomgleichungen lassen sich nun darin unterscheiden, welchen Grad sie besitzen, d.h. welchen Wert n besitzt:

• n=1: lineare Gleichungen
• n=2: quadratische Gleichungen
• n=3: kubische Gleichungen
• n>1: ganz allgemein “nichtlineare Gleichungen”

 
Der Grad n einer Gleichung hat einen wesentlichen Einfluss darauf, mit welchen Verfahren eine Lösung der Gleichung, d.h. die Ermittlung eines Wertes für x, möglich ist.

Lineare Gleichungen lassen sich durch Umstellen nach x ganz einfach analytisch lösen: Aus 0=a0+a1*x wird x=-a0/a1.

Zur Lösung von quadratischen Gleichungen kann die PQ-Formel herangezogen werden. Bei Gleichungen vom Grad 3 oder 4 lassen sich die Cardanischen Formeln verwenden, wobei diese schon sehr kompliziert und unhandlich sind. Im Allgemeinen ist die Lösung von Gleichungen mit einem Grad n>4 gar nicht mehr analytisch möglich, d.h. gibt keine Möglichkeit, die Gleichung mittels Termumformungen (Äquivalenzumformungen) irgendwie nach x umzustellen.

Jetzt kommen numerische Verfahren ins Spiel. Ich definiere wie folgt:

Ein Algorithmus (Rechenvorschrift), der dem Zweck dient, eine mathematische Aufgabe zu lösen, wird als numerisches Lösungsverfahren betrachtet. Ein numerisches Verfahren ist approximativ, falls die Lösung nur angenähert werden kann. Es ist iterativ, falls die Näherung durch mehrfache Ausführung einer Vorschrift schrittweise verbessert wird.

In diesem Beitrag wird mit dem Newtonverfahren ein numerisches Verfahren betrachtet, welches in der Lage ist, nichtlineare Gleichungen approximativ und iterativ zu lösen.
 

Idee des Newtonverfahrens

Wenn wir die Lösung für die oben gezeigte Polynomgleichung suchen, ist das im Prinzip die Suche nach einer Nullstelle für die Polynomfunktion f(x), wenn f(x) wie folgt definiert wird:

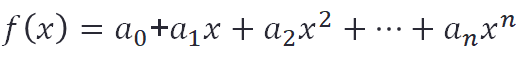
Wir betrachten den folgenden Funktionsgraphen einer Funktion f(x). Die Nullstelle der Funktion (wir benennen sie hier mit dem griechischen Buchstaben “Xi”) ist der Schnittpunkt des Graphen mit der x-Achse.

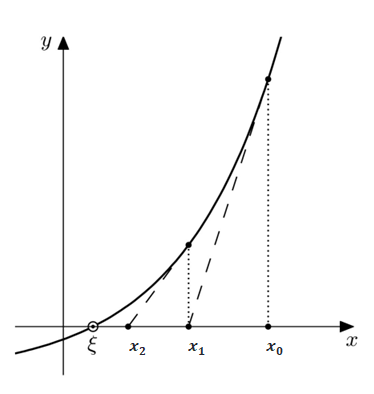
Sehen wir uns den allgemeinen Ablauf des Newtonverfahrens an:

1. Rate einen Ausgangswert x0 in der Nähe der Nullstelle.
2. Bestimme die Tangente an f, die durch x0 verläuft.
3. Bestimme die Nullstelle der Tangente. Dies sei der Wert x1.
4. Wiederhole ab Schritt 2, wobei x1 als neuer Ausgangswert wird.

Mit jeder Wiederholung, d.h. Iteration, rückt der Augangswert näher an die tatsächliche Nullstelle heran. Das Verfahren kann abgebrochen werden, sobald der Ausgangswert eine ausreichende Genauigkeit erreicht hat, d.h. sobald sich der Ausgangswert nur noch in den hinteren Nachkommastellen ändert.

Das Verfahren funktioniert unter folgenden Voraussetzungen:

• Wir betrachten die Funktion f in einem abgeschlossenen Intervall [a,b], in dem sich genau eine Nullstelle befindet. In diesem Fall gilt:
  
• Die Funktion f ist in dem Intervall [a,b] differenzierbar (d.h. wir können die ersten Ableitungen bilden, um die Nullstellen der Tangenten zu berechnen), aber die erste Ableitung f’ ist im ganzen Intervall ungleich 0. Wenn f'(x)=0 ist, bedeutet das nämlich, dass die Tangente an f in x einen Anstieg von 0 hat, also parallel zur x-Achse ist. Diese Tangente hätte dann keine Nullstelle, sodass die Fortsetzung des Newtonverfahrens nicht möglich wäre.

 

Definition des Newtonverfahrens

Sei x0 der erste Ausgangswert. Die Gleichung der Tangente an f in x0 lautet dann:

Umgestellt nach x, ergibt sich:

Dieses x ist der neue Ausgangswert für die nächste Iteration. Ausgedrückt als Folge xn ergibt sich:

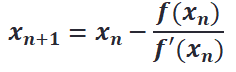
Das ist die allgemeine Newtonvorschrift. Der Grenzwert dieser Folge (wenn n gegen unendlich geht) ist die Nullstelle von f.
 

Rechenbeispiel

Die Aufgabe lautet:

Gegeben ist ein kugelförmiger Tank mit einem Radius von 1,34m und einem Fassungsvermögen von 10 000 Liter.

Im Innern der Tanks soll ein Kontakt angebracht werden, der bei nur noch 1000 Liter Ölmenge ein Warnsignal als Aufforderung für das Nachfüllen gibt.

In welcher Höhe muss der Kontakt angebracht werden?

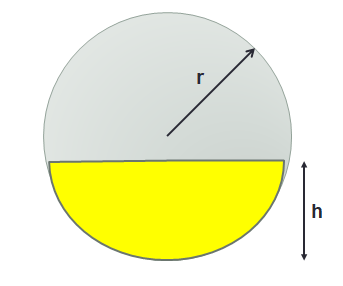
Die Formel für den gelben Kugelabschnitt lautet:

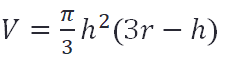
Gesucht ist die Höhe h, wenn ein Volumen V=1m^3 (1000 Liter sind 1 Kubikmeter) und ein Radius r=1,34m gegeben sind. Wir suchen also einen Wert für h zur Lösung der Gleichung 0=(Pi/3)*h^2*(3*r-h)-V. Das entspricht der Suche nach einer Nullstelle für die Funktion f(h) mit eingesetzten Werten:

Die erste Ableitung von f lautet:

Wir raten den Ausgangswert x0=1. Daraus ergeben sich mit der allgemeinen Newtonvorschrift folgende Iterationen:

Wie Ihr seht, gilt h4=h3 und ganz allgemein gilt ab der vierten Iteration: h(n+1)=h(n). Wir haben uns der Nullstelle also mit einer Genauigkeit von 4 Dezimalstellen angenähert. Das sich die Werte nicht mehr ändern, ist auch logisch, denn wenn wir ein h gefunden haben, für das f(h)=0 ist, wird der Term f(h)/f'(h) zu 0.

Ich habe eine Excel-Datei zum Durchrechnen der Iterationen ab einem bestimmten Ausgangswert entwickelt:
MappeNewton

Ihr könnte in der Excel-Datei z.B. den Ausgangswert von 1 auf 0.9 oder 0.5 oder 1.5 ändern: Die Folge xn konvergiert – zumindest für diese Ausgangswerte – immer gegen die Nullstelle 0.5225.

Wenn Ihr aber z.B. 2.1 eingebt, konvergiert die Folge überhaupt nicht.

Bei 2,5 konvergiert die Folge gegen eine andere Nullstelle -0.4616. Eine dritte Nullstelle gibt es bei 3.9601. Die erreicht man z.B. mit dem Ausgangswert 3. Diese beiden Nullstellen kommen nicht als Lösung für die Aufgabenstellung in Frage, denn sie bieten eine Höhe an, die negativ bzw. größer als der Durchmesser des Kugeltanks ist. Fazit: Das Newtonverfahren konvergiert in der Regel nur innerhalb eines begrenzten Intervalls um die Nullstelle herum.

Die Lösung lautet also: Der Kontakt muss in einer Höhe von 0.52m angebracht werden.
 

Konvergenzgeschwindigkeit

Für das Newtonverfahren kann gezeigt werden, dass quadratische Konvergenz vorliegt, d.h

Dabei bezeichnet “x quer” die Nullstelle. Die Voraussetzung dafür ist jedoch, dass die erste Ableitung bei der Nullstelle ungleich 0 ist, d.h. es muss sich um eine sogenannte einfache Nullstelle handeln. Wenn es sich um eine mehrfache Nullstelle handelt, liegt nur noch lineare Konvergenz vor (es sind aber Umformungen zur Wiederherstellung der quadratischen Konvergenz möglich).

Wir gehen davon aus, dass der Abstand zwischen der Nullstelle und xn kleiner als 1 ist. Quadratische Konvergenz bedeutet dann: Sofern schon einige Nachkommastellen korrekt sind, sind im nächsten Näherungswert etwa doppelt so viele Nachkommastellen korrekt. Das lässt sich an dem oben gezeigten Rechenbeispiel nachvollziehen.
 

Anwendung auf Gleichungssysteme

Wir betrachten ein Gleichungssystem mit n Gleichungen:

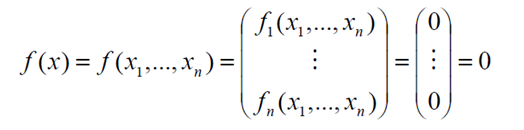
Gesucht wird ein Lösungsvektor x mit n Werten, sodass sich mit den eingesetzten Werten für f1 bis fn 0 ergibt.

Es ist bekannt, dass das Newtonverfahren im 1-dimensionalen Bereich auf die erste Ableitung von f zugreift. Im n-dimensionalen Bereich verwenden wir die Jacobi-Matrix der partiellen Ableitungn von f:

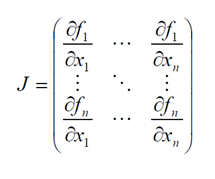
Das Newtonverfahren lässt sich damit wie folgt formulieren:

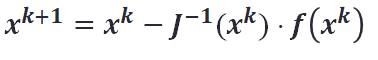
Damit nicht die Inverse der Jacobi-Matrix berechnet werden muss, stellen wir die Gleichung noch etwas um:

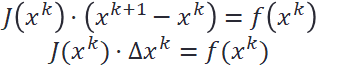
Daraus ergibt sich ein mehrschrittiges Verfahren:

1. Setze x^k in J und f ein
2. Löse das Gleichungssystem J(x^k )*∆x^k=f(x^k) nach ∆x^k
3. Berechne x^(k+1)=x^k+∆x^k
4. Wiederhole ab Schritt 1 bis Abbruch

Das Besondere am n-dimensionalen Newtonverfahren ist, dass in jeder Iteration ein lineares Gleichungssystem gelöst werden muss. Die Lösung eines nichtlinearen Gleichungssystems wird also auf das mehrmalige Lösen von linearen Gleichungssystemen heruntergebrochen.

Um den Aufwand des Verfahrens ein wenig zu reduzieren, kann die Jacobi-Matrix J über mehrere Schritte hinweg konstant beibehalten werden. In diesem Fall müssen nicht in jedem Schritt sämtliche partiellen Ableitungen neu berechnet werden. Die Konvergenzgeschwindigkeit ist in diesem Fall nur noch linear.

 

Fazit

Das Newtonverfahren ist beliebt, weil es eine schnelle (quadratische) Konvergenz bietet. Es sind also in der Regel nicht sehr viele Iterationen nötig, bis man die Nullstelle mit ausreichender Genauigkeit erreicht hat. Der Nachteil des Verfahrens ist die lokale Konvergenz. Während ein Verfahren mit globaler Konvergenz ausgehend von jedem Startwert die Nullstelle erreicht, konvergiert das Newtonverfahren nur für Startwerte in einem bestimmten Intervall um die Nullstelle herum. Außerdem müssen für das Newtonverfahren die Werte der ersten Ableitungen berechnet werden. Dies ist bei anderen Verfahren, wie z.B. beim Sekantenverfahren, nicht notwendig.

Hier findet Ihr meine Powerpoint-Präsentation zum Newton-Verfahren. Es enthält zusätzlich

• den Beweis für die lokale Konvergenz in einem Intervall [a,b] und
• den Beweis für die quadratische Konvergenzgeschwindigkeit.

 
Präsentation: Das Newtonverfahren zur Lösung von Gleichungssystemen